Giải Bài Toán Bài Tập Tự Luận Và Trắc Nghiệm Đại Số Và Giải Tích 11 – Phan Quốc Cường

Tài liệu học tập “Đại số và Giải tích 11” do thầy giáo Phan Quốc Cường biên soạn là một nguồn tài liệu tham khảo toàn diện, với tổng cộng 206 trang. Tài liệu này không chỉ hệ thống hóa kiến thức trọng tâm mà còn phân loại các dạng bài tập một cách khoa học, bao gồm cả bài tập tự luận và trắc nghiệm, giúp học sinh nắm vững và vận dụng kiến thức một cách hiệu quả.

Cấu trúc tài liệu được chia thành 5 chương chính, mỗi chương tập trung vào một chủ đề lớn của chương trình Đại số và Giải tích 11:

Chương 1: HÀM SỐ LƯỢNG GIÁC – PHƯƠNG TRÌNH LƯỢNG GIÁC

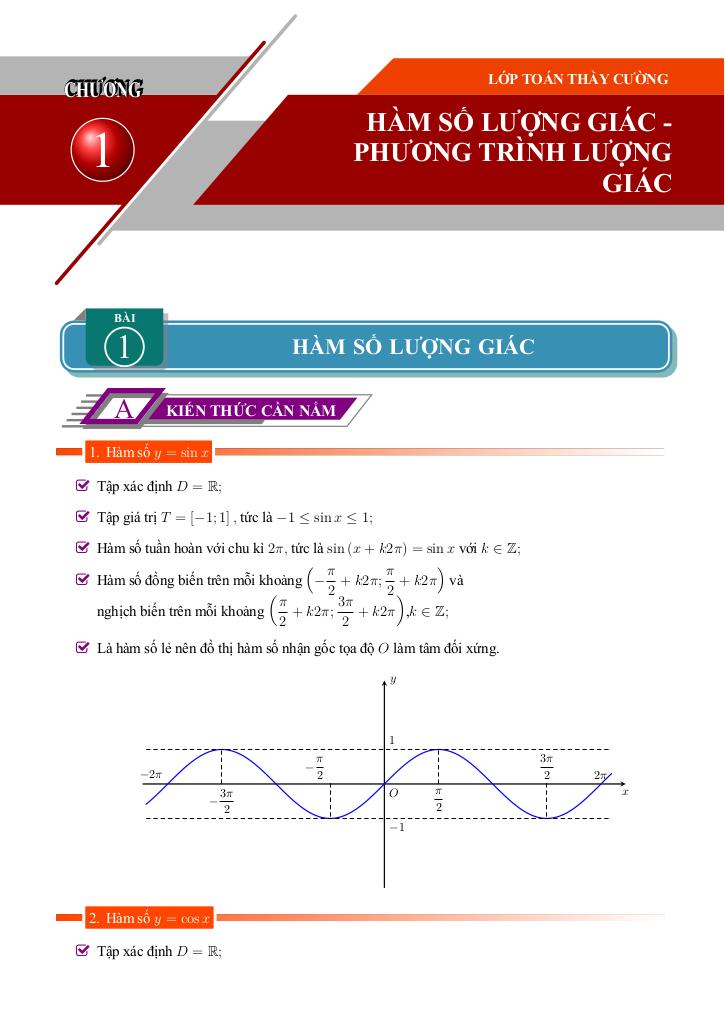
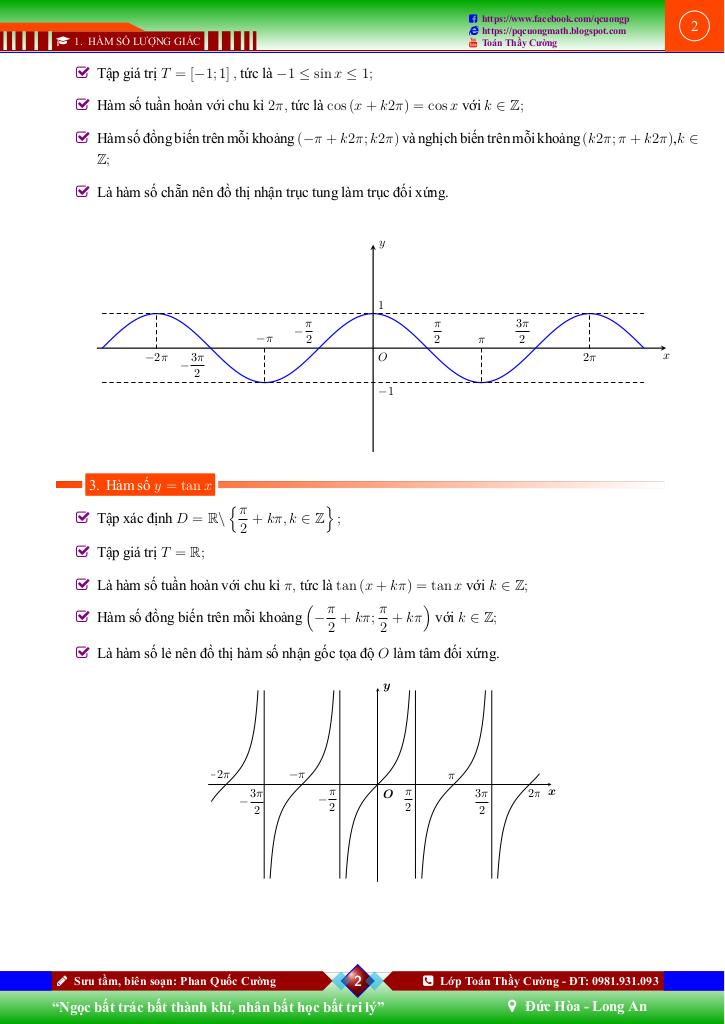
§1 – HÀM SỐ LƯỢNG GIÁC: Tập trung vào kiến thức cơ bản về hàm số lượng giác, tập xác định, tính tuần hoàn, tính chẵn lẻ, tập giá trị và các bài tập liên quan.
§2 – PHƯƠNG TRÌNH LƯỢNG GIÁC: Giải các phương trình lượng giác cơ bản và nâng cao, sử dụng công thức biến đổi để đưa về dạng cơ bản.
§3 – MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP: Giải các phương trình lượng giác đặc biệt như phương trình bậc hai, phương trình tích, phương trình chứa sin x ± cos x và sin giaibaitoan.com x.

Chương 2: TỔ HỢP – XÁC SUẤT

§1 – QUY TẮC ĐẾM: Áp dụng quy tắc cộng và quy tắc nhân để giải các bài toán đếm cơ bản.
§2 – HOÁN VỊ – CHỈNH HỢP – TỔ HỢP: Nắm vững các khái niệm và công thức về hoán vị, chỉnh hợp, tổ hợp và vận dụng vào giải bài tập.
§3 – NHỊ THỨC NEWTON: Sử dụng nhị thức Newton để khai triển và tính toán các biểu thức.
§4 – BIẾN CỐ VÀ XÁC SUẤT CỦA BIẾN CỐ: Hiểu các khái niệm về biến cố, không gian mẫu và tính xác suất của biến cố.

Chương 3: DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN

§1 – NHỊ THỨC NIU-TƠN: Tiếp tục luyện tập và mở rộng kiến thức về nhị thức Newton.
§2 – Dãy Số: Dự đoán công thức tổng quát, xét tính tăng giảm và tính bị chặn của dãy số.
§3 – Cấp Số Cộng: Chứng minh dãy số là cấp số cộng, tính số hạng tổng quát và tổng của n số hạng đầu.
§4 – CẤP SỐ NHÂN: Chứng minh dãy số là cấp số nhân, xác định công bội và số hạng tổng quát, giải các bài toán thực tế liên quan.

Chương 4: GIỚI HẠN

§1 – GIỚI HẠN DÃY SỐ: Chứng minh giới hạn của dãy số bằng định nghĩa và sử dụng các tính chất của giới hạn.
§2 – GIỚI HẠN HÀM SỐ: Tính giới hạn của hàm số tại một điểm và tại vô cực.
§3 – GIỚI HẠN MỘT BÊN CỦA HÀM SỐ: Tính giới hạn một bên của hàm số và ứng dụng vào giải bài tập.
§4 – HÀM SỐ LIÊN TỤC: Xét tính liên tục của hàm số tại một điểm và trên một khoảng.

Chương 5: ĐẠO HÀM

§1 – ĐỊNH NGHĨA ĐẠO HÀM: Tính đạo hàm bằng định nghĩa và xét mối quan hệ giữa liên tục và đạo hàm.
§2 – QUY TẮC TÍNH ĐẠO HÀM: Vận dụng các quy tắc tính đạo hàm để giải bài tập.
§3 – Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM: Viết phương trình tiếp tuyến của đồ thị hàm số.
§4 – ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC: Tính đạo hàm của các hàm số lượng giác.
§5 – ĐẠO HÀM CẤP CAO: Tính đạo hàm cấp cao của hàm số.
§6 – VI PHÂN: Hiểu khái niệm và ứng dụng của vi phân.

Điểm nổi bật của tài liệu là sự phân loại bài tập theo dạng, giúp học sinh dễ dàng nhận diện và áp dụng phương pháp giải phù hợp. Mỗi dạng bài tập đều có phần bài tập tự luận và trắc nghiệm, kèm theo đáp án chi tiết, tạo điều kiện thuận lợi cho việc tự học và ôn luyện.

Đánh giá chung: Tài liệu là một công cụ hỗ trợ học tập hữu ích cho học sinh lớp 11, đặc biệt là những em muốn củng cố kiến thức và nâng cao kỹ năng giải toán. Cách trình bày rõ ràng, mạch lạc, cùng với hệ thống bài tập đa dạng và đáp án chi tiết, giúp học sinh tự tin hơn trong quá trình học tập và làm bài thi.